[백준] 17103번 골드바흐 파티션 | 파이썬 Python

문제

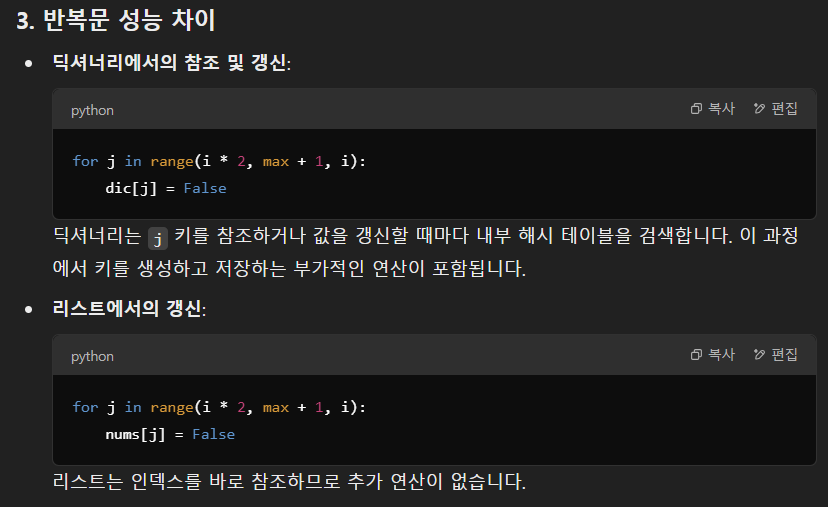
• 골드바흐의 추측: 2보다 큰 짝수는 두 소수의 합으로 나타낼 수 있다.

짝수 N을 두 소수의 합으로 나타내는 표현을 골드바흐 파티션이라고 한다. 짝수 N이 주어졌을 때, 골드바흐 파티션의 개수를 구해보자. 두 소수의 순서만 다른 것은 같은 파티션이다.

 

입력

첫째 줄에 테스트 케이스의 개수 T (1 ≤ T ≤ 100)가 주어진다. 각 테스트 케이스는 한 줄로 이루어져 있고, 정수 N은 짝수이고, 2 < N ≤ 1,000,000을 만족한다.

 

출력

각각의 테스트 케이스마다 골드바흐 파티션의 수를 출력한다.

 

예제

 

나의 풀이1

max = 1000000
dic =  {i : True for i in range(2, max + 1)}

for i in range(2, int(max**0.5) + 1):
    cnt = 2
    while i * cnt <= max:
        if dic[i*cnt]:
            dic[i*cnt] = False
        cnt += 1

T = int(input())  

for _ in range(T):
    num = int(input())
    nums = []

    for i in range(2, num + 1):
        if dic[i]:
            nums.append(i)
    
    cnt = 0

    for j in range(len(nums)):
        for k in range(j, len(nums)):
            if nums[j] + nums[k] == num:
                cnt += 1
                
    print(cnt)

• 입력값의 최댓값을 길이로 가지는 딕셔너리를 만들어서 에라토스테네스의 체를 사용해 소수인지를 판별했다.
• 그후 각각의 입력값마다 해당하는 소수를 리스트에 담아서 모든 경우의 수를 실행해서 카운트를 셌다.
• 이 풀이는 당연하게도 시간초과로 실패했다.

 

나의 풀이2

import sys
input = sys.stdin.readline

max = 1000000
dic =  {i : True for i in range(2, max + 1)}

for i in range(2, int(max**0.5) + 1):
    if dic[i]:
        for j in range(i * 2, max + 1, i):
            dic[j] = False

T = int(input())  

for _ in range(T):
    N = int(input())
    cnt = 0

    for i in range(2, N // 2 + 1):
        if dic[i] and dic[N-i]:
            cnt += 1
    
    print(cnt)

• 동일하게 딕셔너리를 사용하지만 입력값마다 골드바흐 파티션의 개수를 탐색하는 부분을 수정했다.
• 입력값의 절반만 for문을 실행해서 개수를 카운트한다.
  • 예를 들면 `N`이 `10`이고 `i`가 `3`일 때, `i`와 `N-i`가 소수라면, 즉 `3`과 `7`이 소수라면 골드바흐 파티션에 해당한다.
  • 이렇게 정수 `N`을 절반으로 나눠서 양 끝에서부터 하나씩 탐색한다.
• 하지만 이 풀이도 시간초과로 실패했다.

 

나의 풀이3

import sys
input = sys.stdin.readline

max = 1000000
nums = [True]*(max+1)

for i in range(2, int(max**0.5)+1):
    if nums[i]:
        for j in range(i*2, max+1, i):
            nums[j] = False

T = int(input())

for _ in range(T):
    N = int(input())
    cnt = 0

    for i in range(2, N//2+1):
        if nums[i] and nums[N-i]:
            cnt += 1
    
    print(cnt)

• 딕셔너리가 아닌 리스트를 사용했다.
• 이 풀이로 드디어 테스트를 통과할 수 있었다.
• 딕셔너리가 해시테이블을 사용하기 때문에 무조건 리스트보다 빠를 거라고 생각했었는데 아니었다. 숫자를 인덱스로 다루는 경우에는 리스트가 메모리적으로 효율적이고 속도도 빠르다고 한다.