문제
https://www.acmicpc.net/problem/9251
LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다.
예를 들어, ACAYKP와 CAPCAK의 LCS는 ACAK가 된다.
입력
첫째 줄과 둘째 줄에 두 문자열이 주어진다. 문자열은 알파벳 대문자로만 이루어져 있으며, 최대 1000글자로 이루어져 있다.
출력
첫째 줄에 입력으로 주어진 두 문자열의 LCS의 길이를 출력한다.
예제

다른 사람의 풀이
A = input()
B = input()
dp = [[0] * (len(B)+1) for _ in range(len(A)+1)]
for i in range(1, len(A)+1):
for j in range(1, len(B)+1):
if A[i-1] == B[j-1]:
dp[i][j] = dp[i-1][j-1] + 1
else:
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
print(dp[-1][-1])DP 테이블 초기화
두 문자열을 비교하기 위해 2차원 리스트를 생성한다.
`dp[i][j]`는 `A[0:i]`와 `B[0:j]`를 비교했을 때의 최장 공통 부분 수열의 길이를 의미한다.
예를 들어 "ACAYKP", "CAPCAK" 두 문자열에 대해
`dp[2][4]`는 "AC"와 "CAPC" 두 문자열 사이의 LCS의 길이를 의미한다.
LCS 알고리즘
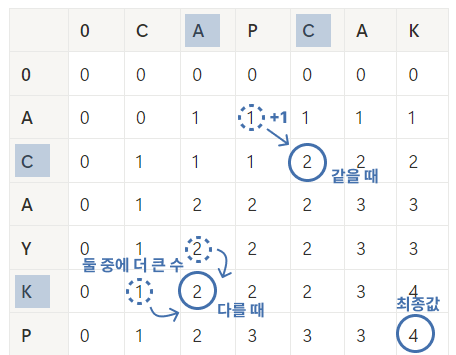
문자가 같을 때 `dp[i][j] = dp[i-1][j-1] + 1`
-> 공통 문자를 하나 더 찾았기 때문에, 이전까지의 LCS 길이에 1을 더한다.
문자가 다를 때 `dp[i][j] = max(dp[i-1][j], dp[i][j-1])`
현재 문자를 제외한 상태 중 가장 긴 LCS를 선택한다.
예를 들어 `dp[3][3]`일 때, `dp[2][3]`과 `dp[3][2]`을 비교한다.
즉, 하나는 A의 문자만 제외, 다른 하나는 B의 문자만 제외한 상태로 비교하는 것이다.
예를 들어 문자열 A = "ACB", B = "ABA"의
`dp[3][3]` "B"와 "A"는 일치하지 않는다.
그렇다면 두 가지 선택지 중 더 큰 값을 선택해야 한다.
"AC" vs "ABA" → LCS: "A" (길이 1)
"ACB" vs "AB" → LCS: "AB" (길이 2)
→ 두 가지 경우 중 더 긴 "AB"를 선택해서 `dp[3][3] = 2`로 결정한다.
참고

